B站左神之前牛客网直播的教程 时间复杂度，递归，对数器等基础知识点

认识时间复杂度

时间复杂度为一个算法流程中，常数操作数量的一个指标。常用O(读作big O)来表示。具体 来说，先要对一个算法流程非常熟悉，然后去写出这个算法流程中，发生了多少常数操作， 进而总结出常数操作数量的表达式。

在表达式中，只要高阶项，不要低阶项，也不要高阶项的系数，剩下的部分如果为f(N)，那 么时间复杂度为O(f(N))。

评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行 时间，也就是“常数项时间”。

常数操作

一个操作如果和样本的数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作。例如+-*/

异或运算

  1. 0^N == N N^N == 0
  2. 异或运算满足交换律和结合率
  3. 不用额外变量交换两个数
  4. 一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到这一个数
  5. 一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到这两个数

a、b在内存中是两块独立的区域时(分别指向不同的内存)：↓

image-20211118230556869

异或面试题
1) 数组里有一种数出现了奇数次，其他数出现了偶数次
2) 数组里有两种数出现了奇数次，其他数偶数次

image-20211118230932840

1的解法

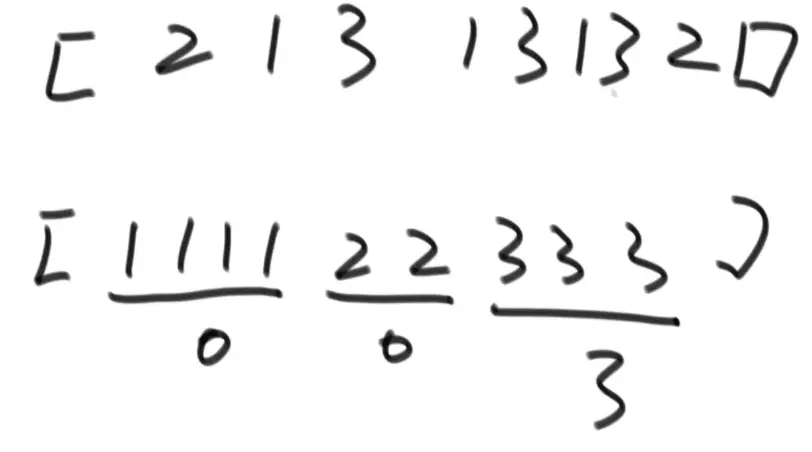
image-20211118231126071

public static void printOddTimesNum1(int[] arr) {  
   int eO = 0;  
   for (int cur : arr) {  
      eO ^= cur;  
   }  
   System.out.println(eO);  
}

异或运算跟顺序没关系，跟1出现的次数有关（偶奇数）用无进位相加来理解

2的解法

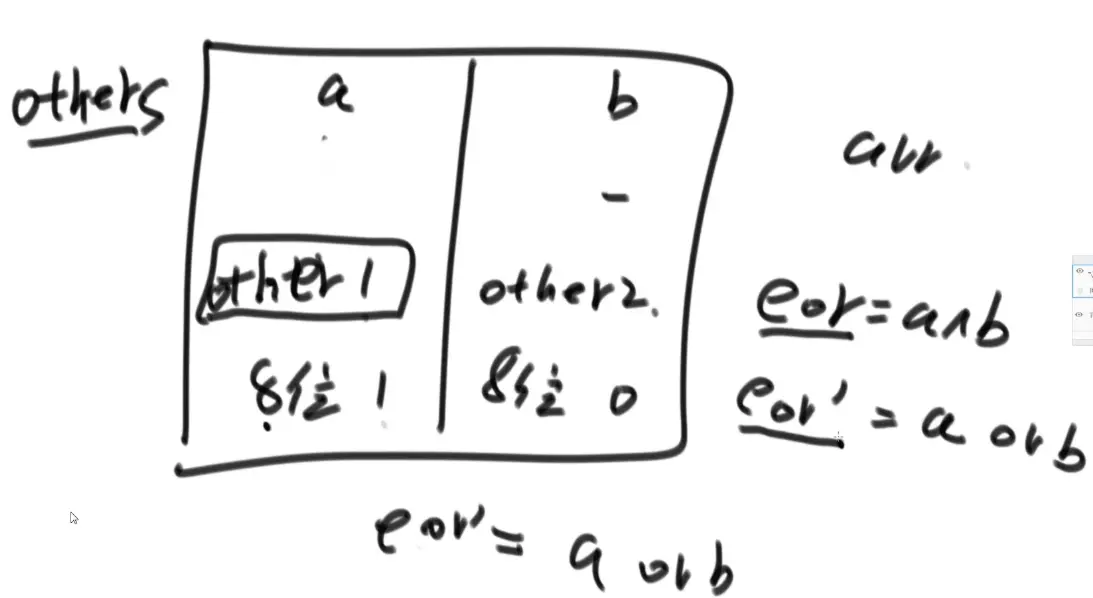
eor 异或所有数

eor’ 只异或 第n位不为1的数

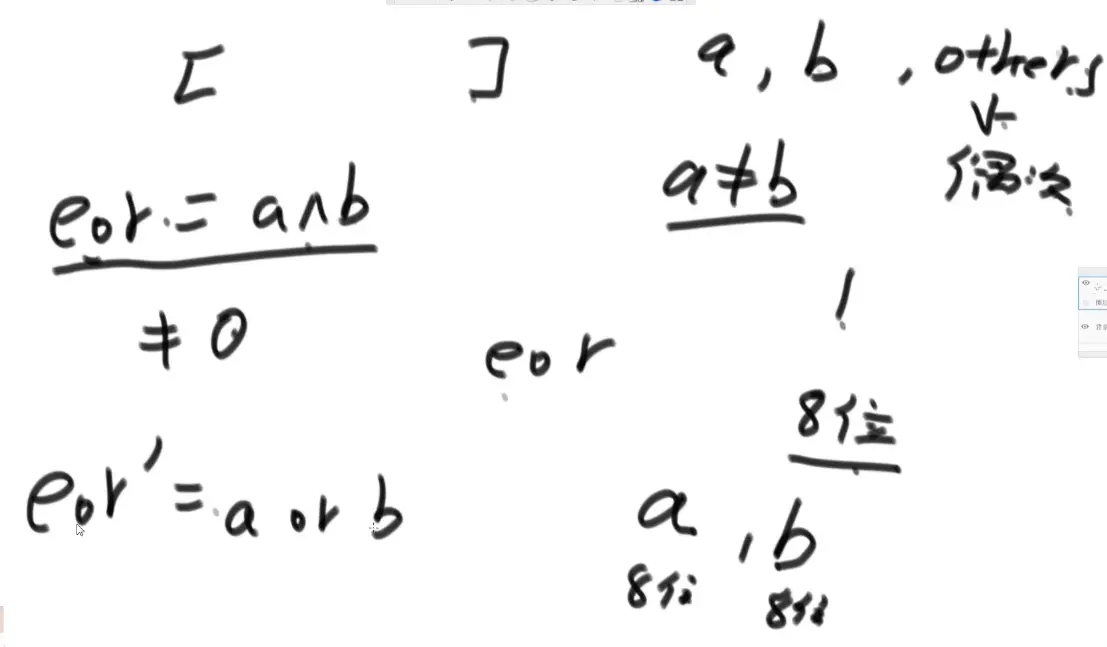
image-20211122204440652

然后将eor^eor'

image-20211122204636891

public static void printOddTimesNum2(int[] arr) {  
   int eO = 0, eOhasOne = 0;  
   for (int curNum : arr) {  
      eO ^= curNum;  
   }  
   int rightOne = eO & (~eO + 1);  
   for (int cur : arr) {  
      if ((cur & rightOne) != 0) {  
         eOhasOne ^= cur;  
      }  
   }  
   System.out.println(eOhasOne + " " + (eO ^ eOhasOne));  
}
提取最右的1

image-20211122210212052

对数器

对数器的概念和使用

  1. 有一个你想要测的方法a
  2. 实现复杂度不好但是容易实现的方法b
  3. 实现一个随机样本产生器 4，把方法a和方法b跑相同的随机样本，看看得到的结果是否一样
  4. 如果有一个随机样本使得比对结果不一致，打印样本进行人工干预，改对方法a或者 方法b
  5. 当样本数量很多时比对测试依然正确，可以确定方法a已经正确。

递归

public static int getMax(int[] arr) {  
   return process(arr, 0, arr.length - 1);  
}  
  
public static int process(int[] arr, int L, int R) {  
   if (L == R) {  
      return arr[L];  
   }  
   int mid = L + ((R - L) >> 1);  
   int leftMax = process(arr, L, mid);  
   int rightMax = process(arr, mid + 1, R);  
   return Math.max(leftMax, rightMax);  
}

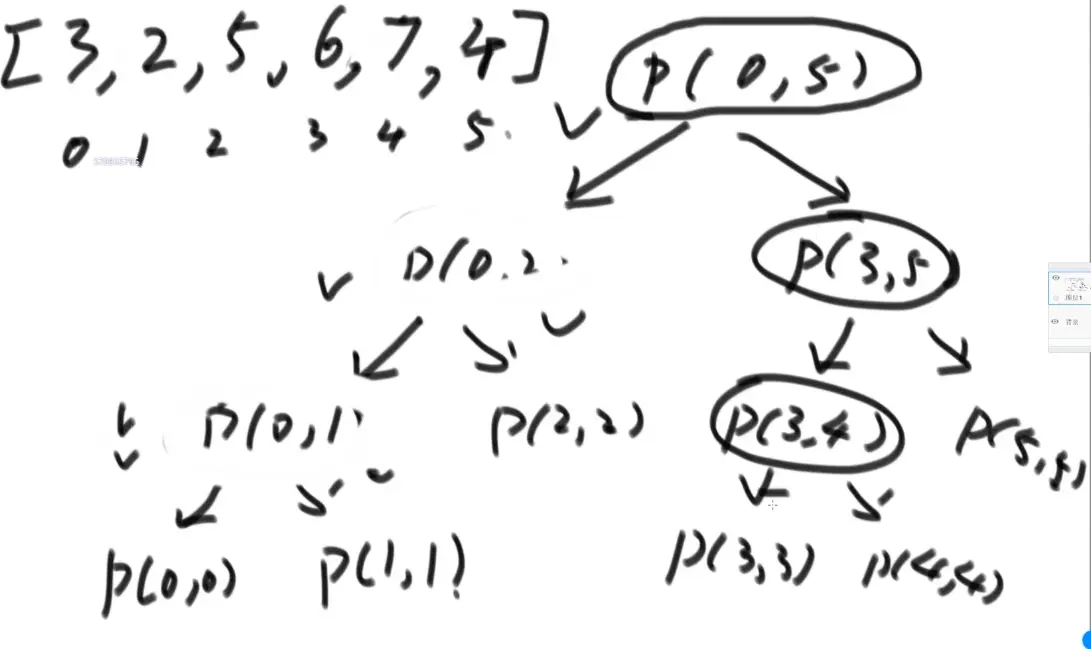
image-20211122215458967

master 公式

用递归方法找一个数组中的最大值，系统上到底是怎么做的? master公式的使用
T(N) = a*T(N/b) + O(N^d)

  1. log(b,a) > d -> 复杂度为O(N^log(b,a))
  2. log(b,a) = d -> 复杂度为O(N^d * logN)
  3. log(b,a) < d -> 复杂度为O(N^d)

补充阅读:www.gocalf.com/blog/algorithm-complexity-and-master- theorem.html image-20211122215805539

子问题必须等规模

1/2 + 1/2 行

1/3 + 2/3 不行

比较器

  1. 比较器的实质就是重载比较运算符
  2. 比较器可以很好的应用在特殊标准的排序上
  3. 比较器可以很好的应用在根据特殊标准排序的结构上