贪心算法
贪心算法
贪心算法
在某一个标准下,优先考虑最满足标准的样本,最后考虑最不满足标准的样本,最终得到 一个答案的算法,叫作贪心算法。
也就是说,不从整体最优上加以考虑,所做出的是在某种意义上的局部最优解。 局部最优 -?-> 整体最优
贪心算法的在笔试时的解题套路
- 实现一个不依靠贪心策略的解法X,可以用最暴力的尝试
- 脑补出贪心策略A、贪心策略B、贪心策略C…
- 用解法X和对数器,去验证每一个贪心策略,用实验的方式得知哪个贪心策略正确
- 不要去纠结贪心策略的证明
证明贪心算法
证明比较有传递性(有效比较)
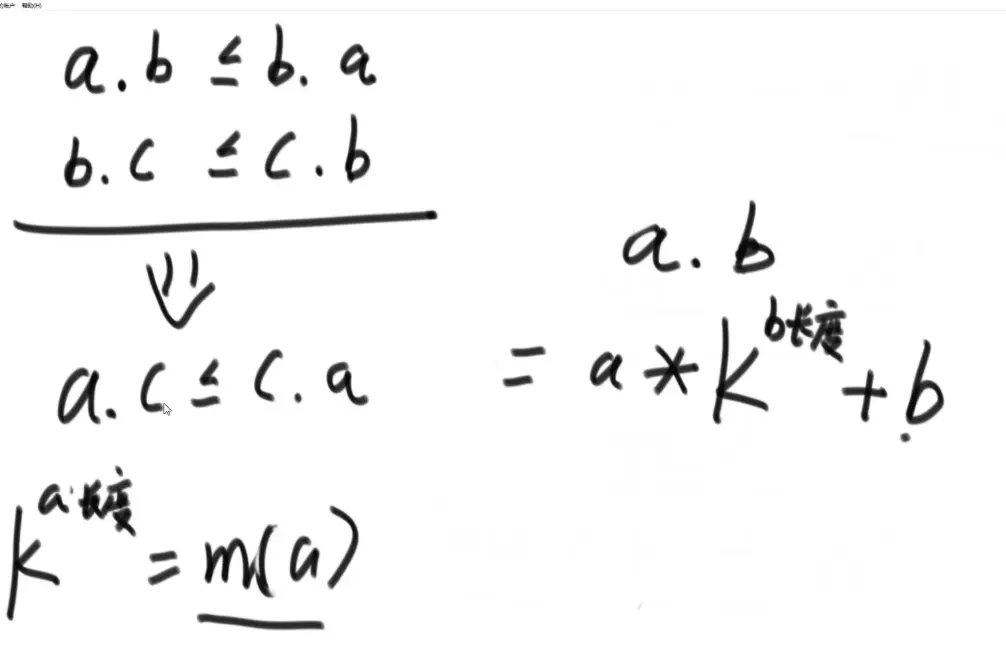
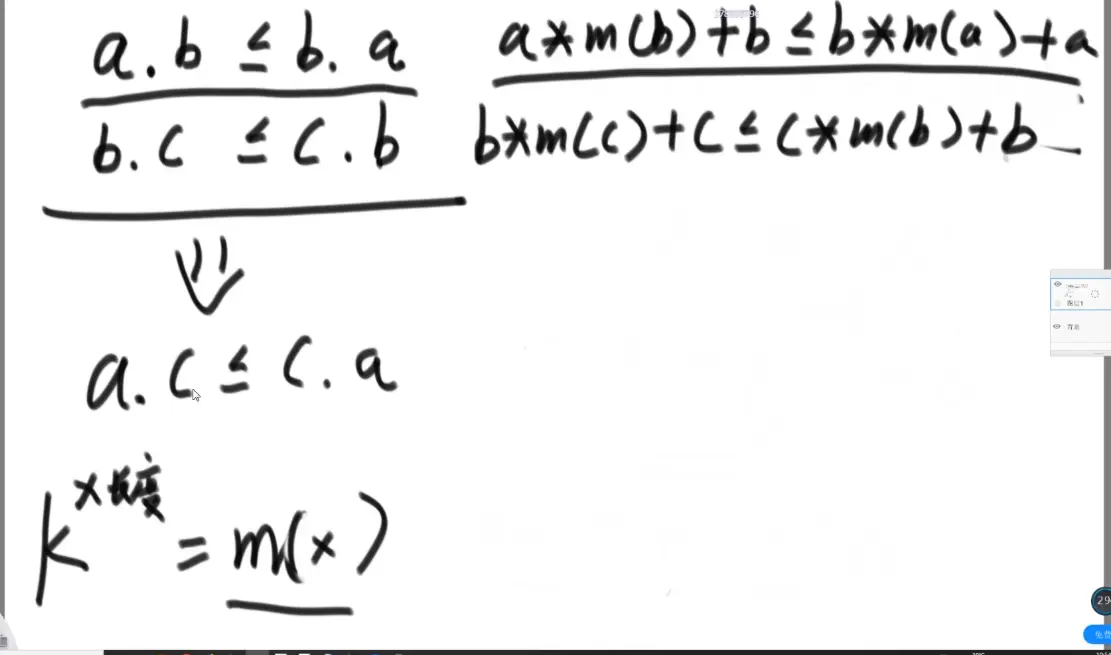
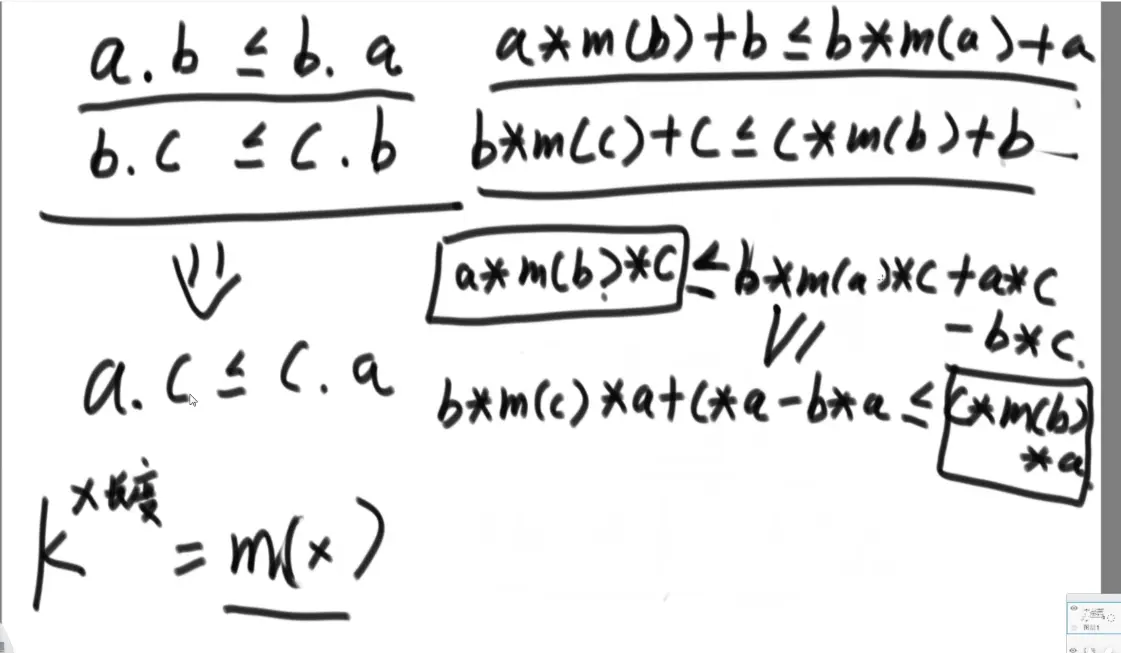

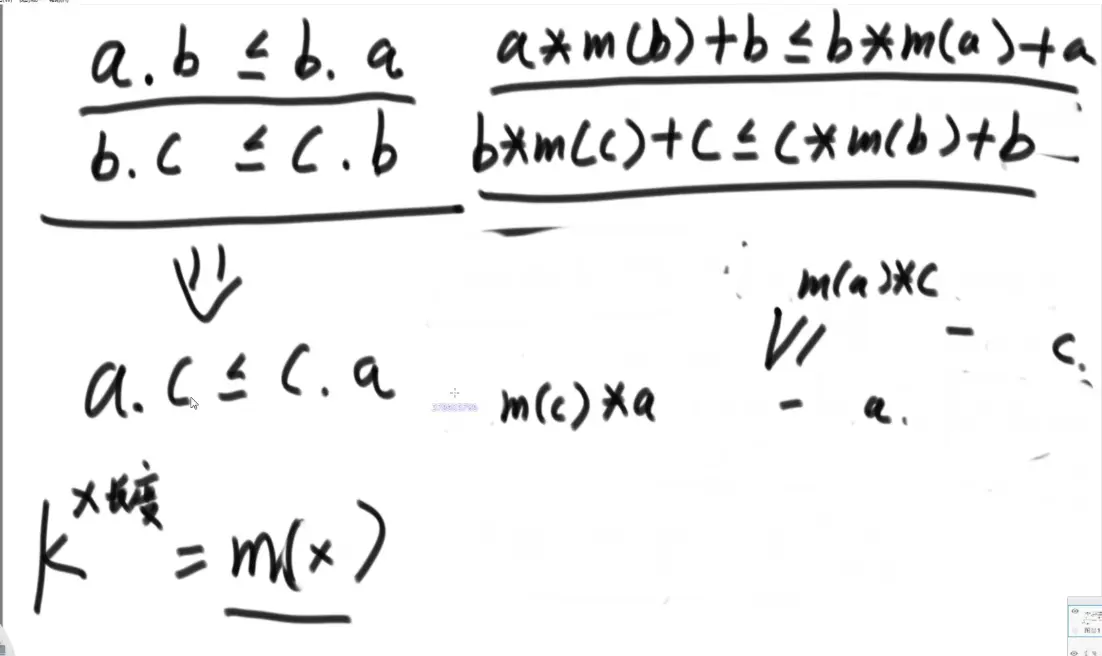

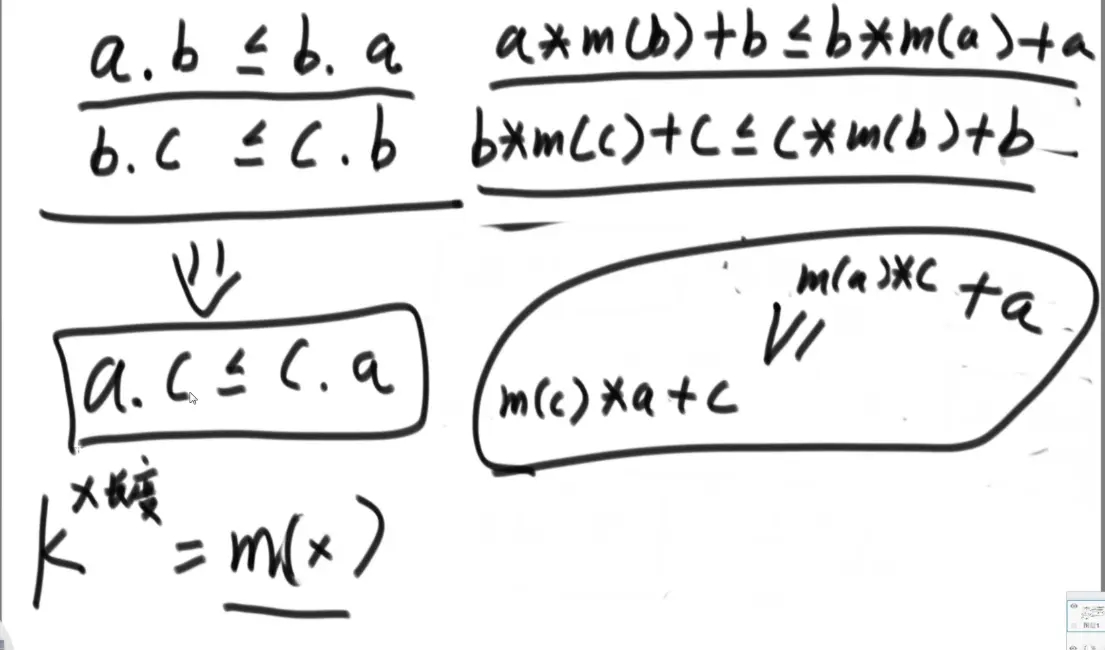
所以 :前 后 < 后 前
证明原始数据中任意两个字母交换都是成立的:a m1 m2 b < b m1 m2 a
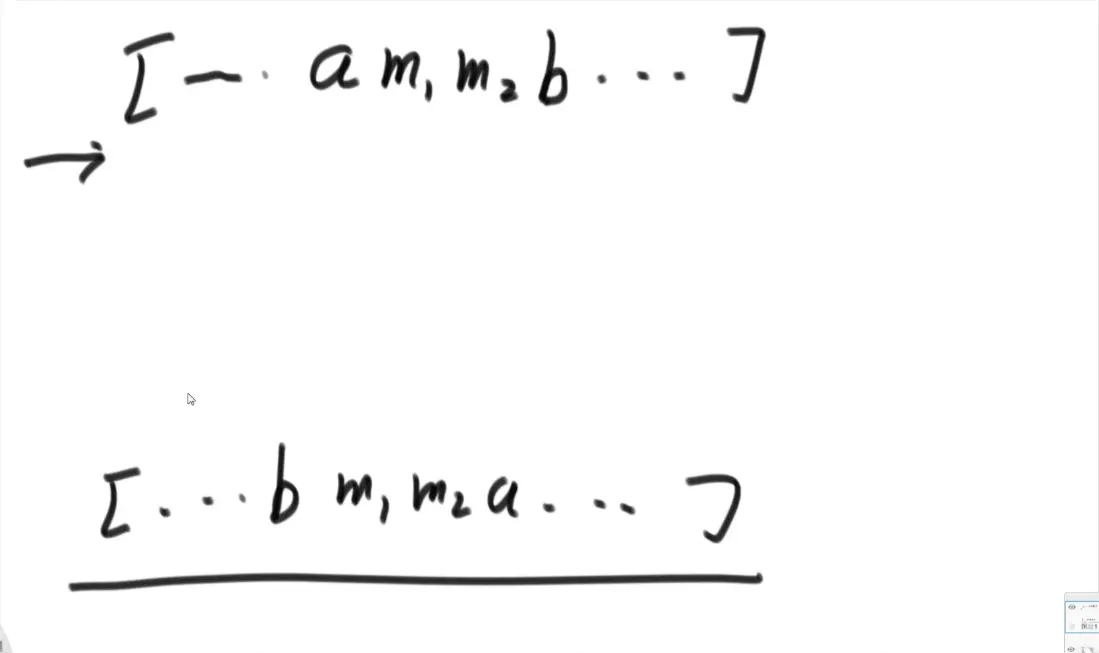


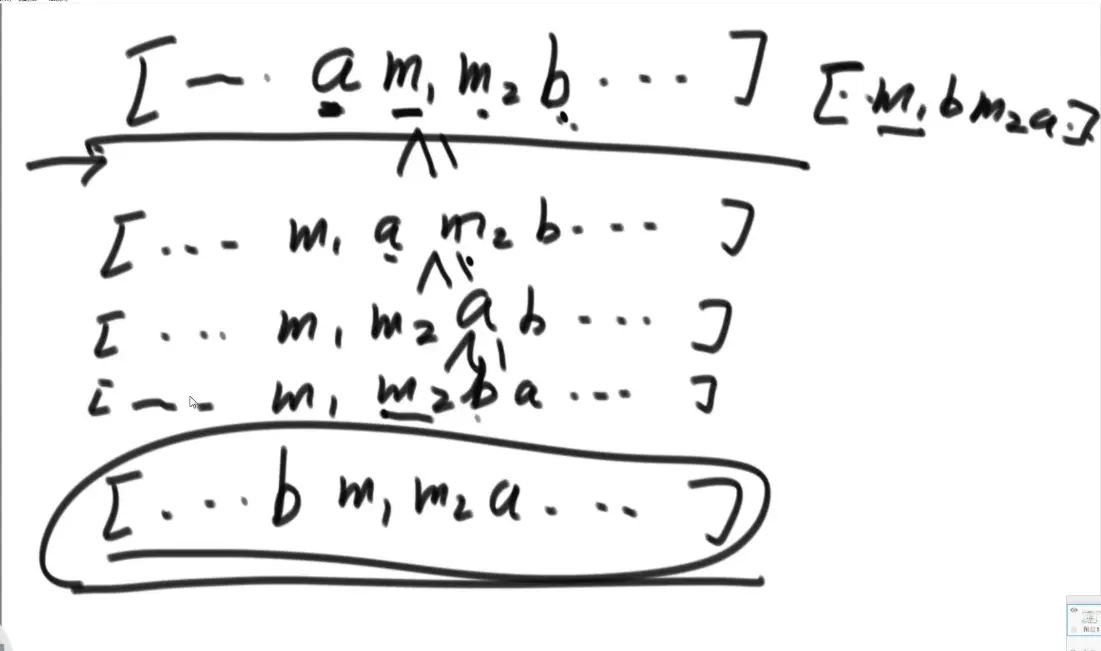
最后证明任意位置任意数量交换 前<后
常见题目
切金条
一块金条切成两半,是需要花费和长度数值一样的铜板的。比如长度为20的金条,不管切成长度多大的两半,都要花费20个铜板。
一群人想整分整块金条,怎么分最省铜板? 例如,给定数组{10,20,30},代表一共三个人,整块金条长度为10+20+30=60。 金条要分成10,20,30三个部分。 如果先把长度60的金条分成10和50,花费60; 再把长度50的金条分成20和30,花费50;一共花费110铜板。 但是如果先把长度60的金条分成30和30,花费60;再把长度30金条分成10和20, 花费30;一共花费90铜板。
输入一个数组,返回分割的最小代价。
public static int lessMoney(int[] arr) {
PriorityQueue<Integer> pQ = new PriorityQueue<>();
for (int i = 0; i < arr.length; i++) {
pQ.add(arr[i]);
}
int sum = 0;
int cur = 0;
while (pQ.size() > 1) {
cur = pQ.poll() + pQ.poll();
sum += cur;
pQ.add(cur);
}
return sum;
}
public static class MinheapComparator implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2; // < 0 o1 < o2 负数
}
}
public static class MaxheapComparator implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1; // < o2 < o1
}
}
public static void main(String[] args) {
// solution
int[] arr = { 6, 7, 8, 9 };
System.out.println(lessMoney(arr));
int[] arrForHeap = { 3, 5, 2, 7, 0, 1, 6, 4 };
// min heap
PriorityQueue<Integer> minQ1 = new PriorityQueue<>();
for (int i = 0; i < arrForHeap.length; i++) {
minQ1.add(arrForHeap[i]);
}
while (!minQ1.isEmpty()) {
System.out.print(minQ1.poll() + " ");
}
System.out.println();
// min heap use Comparator
PriorityQueue<Integer> minQ2 = new PriorityQueue<>(new MinheapComparator());
for (int i = 0; i < arrForHeap.length; i++) {
minQ2.add(arrForHeap[i]);
}
while (!minQ2.isEmpty()) {
System.out.print(minQ2.poll() + " ");
}
System.out.println();
// max heap use Comparator
PriorityQueue<Integer> maxQ = new PriorityQueue<>(new MaxheapComparator());
for (int i = 0; i < arrForHeap.length; i++) {
maxQ.add(arrForHeap[i]);
}
while (!maxQ.isEmpty()) {
System.out.print(maxQ.poll() + " ");
}
}
会议安排
一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目的宣讲。 给你每一个项目开始的时间和结束的时间(给你一个数 组,里面是一个个具体 的项目),你来安排宣讲的日程,要求会议室进行的宣讲的场次最多。 返回这个最多的宣讲场次。
最优解:优先安排结束时间早的会议
能明显举出反例的直接pass
public static class Program {
public int start;
public int end;
public Program(int start, int end) {
this.start = start;
this.end = end;
}
}
public static class ProgramComparator implements Comparator<Program> {
@Override
public int compare(Program o1, Program o2) {
return o1.end - o2.end;
}
}
public static int bestArrange(Program[] programs, int start) {
Arrays.sort(programs, new ProgramComparator());
int result = 0;
for (int i = 0; i < programs.length; i++) {
if (start <= programs[i].start) {
result++;
start = programs[i].end;
}
}
return result;
}
创业最大收益
输入:
正数数组costs
正数数组profits
正数k
正数m
含义:
costs[i]表示i号项目的花费 profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润) k表示你只能串行的最多做k个项目
m表示你初始的资金
说明: 你每做完一个项目,马上获得的收益,可以支持你去做下一个项目。 输出:
你最后获得的最大钱数。
public class Code05_IPO {
public static class Node {
public int p;
public int c;
public Node(int p, int c) {
this.p = p;
this.c = c;
}
}
public static class MinCostComparator implements Comparator<Node> {
@Override
public int compare(Node o1, Node o2) {
return o1.c - o2.c;
}
}
public static class MaxProfitComparator implements Comparator<Node> {
@Override
public int compare(Node o1, Node o2) {
return o2.p - o1.p;
}
}
public static int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) {
Node[] nodes = new Node[Profits.length];
for (int i = 0; i < Profits.length; i++) {
nodes[i] = new Node(Profits[i], Capital[i]);
}
PriorityQueue<Node> minCostQ = new PriorityQueue<>(new MinCostComparator());
PriorityQueue<Node> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());
for (int i = 0; i < nodes.length; i++) {
minCostQ.add(nodes[i]);
}
for (int i = 0; i < k; i++) {
while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) {
maxProfitQ.add(minCostQ.poll());
}
if (maxProfitQ.isEmpty()) {
return W;
}
W += maxProfitQ.poll().p;
}
return W;
}
}
一个数据流,随时能取中位数 (非贪心算法题
private PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(new MaxHeapComparator());
private PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>(new MinHeapComparator());
private void modifyTwoHeapsSize() {
if (this.maxHeap.size() == this.minHeap.size() + 2) {
this.minHeap.add(this.maxHeap.poll());
}
if (this.minHeap.size() == this.maxHeap.size() + 2) {
this.maxHeap.add(this.minHeap.poll());
}
}
public void addNumber(int num) {
if (maxHeap.isEmpty() || num <= maxHeap.peek()) {
maxHeap.add(num);
} else {
minHeap.add(num);
}
modifyTwoHeapsSize();
}
public Integer getMedian() {
int maxHeapSize = this.maxHeap.size();
int minHeapSize = this.minHeap.size();
if (maxHeapSize + minHeapSize == 0) {
return null;
}
Integer maxHeapHead = this.maxHeap.peek();
Integer minHeapHead = this.minHeap.peek();
if (((maxHeapSize + minHeapSize) & 1) == 0) {
return (maxHeapHead + minHeapHead) / 2;
}
return maxHeapSize > minHeapSize ? maxHeapHead : minHeapHead;
}
}
n皇后
N皇后问题是指在N*N的棋盘上要摆N个皇后,要求任何两个皇后不同行、不同列, 也不在同一条斜线上。
给定一个整数n,返回n皇后的摆法有多少种。
n=1,返回1。
n=2或3,2皇后和3皇后问题无论怎么摆都不行,返回0。 n=8,返回92。
package class08;
public class Code09_NQueens {
public static int num1(int n) {
if (n < 1) {
return 0;
}
int[] record = new int[n];
return process1(0, record, n);
}
public static int process1(int i, int[] record, int n){
if (i == n) {
return 1;
}
int res = 0;
for (int j = 0; j < n; j++) {
if (isValid(record, i, j)) {
record[i] = j;
res += process1(i + 1, record, n);
}
}
return res;
}
public static boolean isValid(int[] record, int i, int j) {
for (int k = 0; k < i; k++) {
if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
return false;
}
}
return true;
}
public static int num2(int n) {
if (n < 1 || n > 32) {
return 0;
}
int upperLim = n == 32 ? -1 : (1 << n) - 1;
return process2(upperLim, 0, 0, 0);
}
public static int process2(int upperLim, int colLim, int leftDiaLim,
int rightDiaLim) {
if (colLim == upperLim) {
return 1;
}
int pos = 0;
int mostRightOne = 0;
pos = upperLim & (~(colLim | leftDiaLim | rightDiaLim));
int res = 0;
while (pos != 0) {
mostRightOne = pos & (~pos + 1);
pos = pos - mostRightOne;
res += process2(upperLim, colLim | mostRightOne,
(leftDiaLim | mostRightOne) << 1,
(rightDiaLim | mostRightOne) >>> 1);
}
return res;
}
public static void main(String[] args) {
int n = 14;
long start = System.currentTimeMillis();
System.out.println(num2(n));
long end = System.currentTimeMillis();
System.out.println("cost time: " + (end - start) + "ms");
start = System.currentTimeMillis();
System.out.println(num1(n));
end = System.currentTimeMillis();
System.out.println("cost time: " + (end - start) + "ms");
}
}



