二叉树
二叉树
节点结构
class Node< > { V value; Node left; Node right; } 用递归和非递归两种方式实现二叉树的先序、中序、后序遍历 如何直观的打印一颗二叉树 如何完成二叉树的宽度优先遍历(常见题目:求一棵二叉树的宽度)
递归序
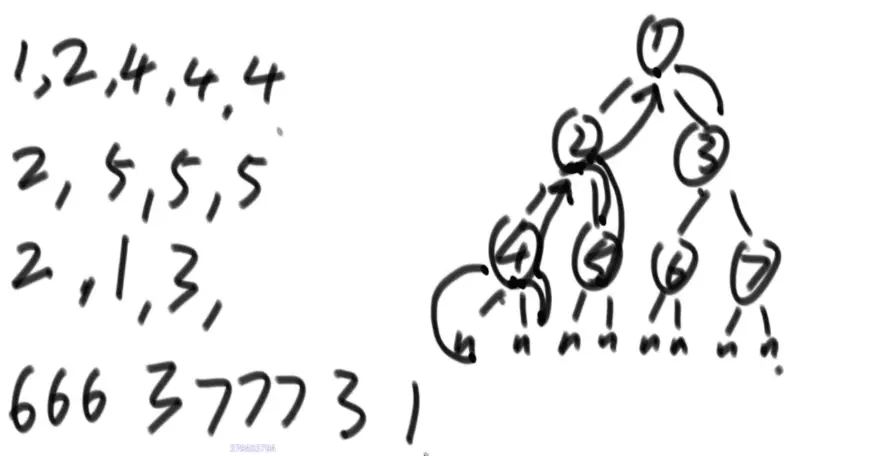
先中后打印二叉树
递归

根据递归序,每个节点都要经历三次,所以先序就在第一次的时候打印,中-》第二次,后-》第三次
public static void preOrderRecur(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}
public static void posOrderRecur(Node head) {
if (head == null) {
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}
非递归:栈
- 前序
public static void preOrderUnRecur(Node head) {
System.out.print("pre-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
中序
public static void inOrderUnRecur(Node head) {
System.out.print("in-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
2.后序:在一的前提下设置收集栈 存放一的数据 再打印收集栈就是一的逆序 即后序
public static void posOrderUnRecur1(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop();
s2.push(head);
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}
public static void posOrderUnRecur2(Node h) {
System.out.print("pos-order: ");
if (h != null) {
Stack<Node> stack = new Stack<Node>();
stack.push(h);
Node c = null;
while (!stack.isEmpty()) {
c = stack.peek();
if (c.left != null && h != c.left && h != c.right) {
stack.push(c.left);
} else if (c.right != null && h != c.right) {
stack.push(c.right);
} else {
System.out.print(stack.pop().value + " ");
h = c;
}
}
}
System.out.println();
}
如何直观打印一棵树
public static void printTree(Node head) {
System.out.println("Binary Tree:");
printInOrder(head, 0, "H", 17);
System.out.println();
}
public static void printInOrder(Node head, int height, String to, int len) {
if (head == null) {
return;
}
printInOrder(head.right, height + 1, "v", len);
String val = to + head.value + to;
int lenM = val.length();
int lenL = (len - lenM) / 2;
int lenR = len - lenM - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printInOrder(head.left, height + 1, "^", len);
}
层遍历
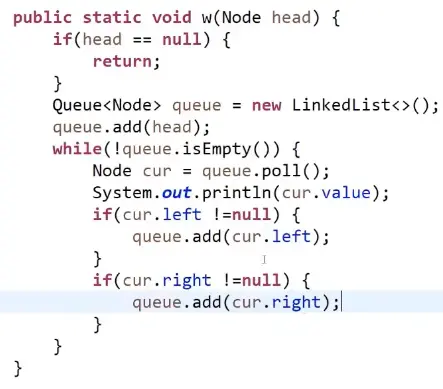
求最大宽度和层数
public static int getMaxWidth(Node head) {
if (head == null) {
return 0;
}
int maxWidth = 0;
int curWidth = 0;
int curLevel = 0;
HashMap<Node, Integer> levelMap = new HashMap<>();
levelMap.put(head, 1);
LinkedList<Node> queue = new LinkedList<>();
queue.add(head);
Node node = null;
Node left = null;
Node right = null;
while (!queue.isEmpty()) {
node = queue.poll();
left = node.left;
right = node.right;
if (left != null) {
levelMap.put(left, levelMap.get(node) + 1);
queue.add(left);
}
if (right != null) {
levelMap.put(right, levelMap.get(node) + 1);
queue.add(right);
}
if (levelMap.get(node) > curLevel) {
curWidth = 0;
curLevel = levelMap.get(node);
} else {
curWidth++;
}
maxWidth = Math.max(maxWidth, curWidth);
}
return maxWidth;
}
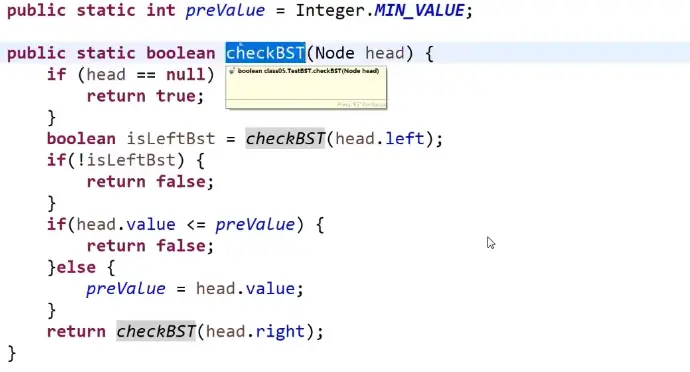
如何判断一棵树是搜索二叉树
中序遍历 值保持增序
递归
public static boolean isBST(Node head) {
if (head == null) {
return true;
}
LinkedList<Node> inOrderList = new LinkedList<>();
process(head, inOrderList);
int pre = Integer.MIN_VALUE;
for (Node cur : inOrderList) {
if (pre >= cur.value) {
return false;
}
pre = cur.value;
}
return true;
}
public static void process(Node node, LinkedList<Node> inOrderList) {
if (node == null) {
return;
}
process(node.left, inOrderList);
inOrderList.add(node);
process(node.right, inOrderList);
}
迭代
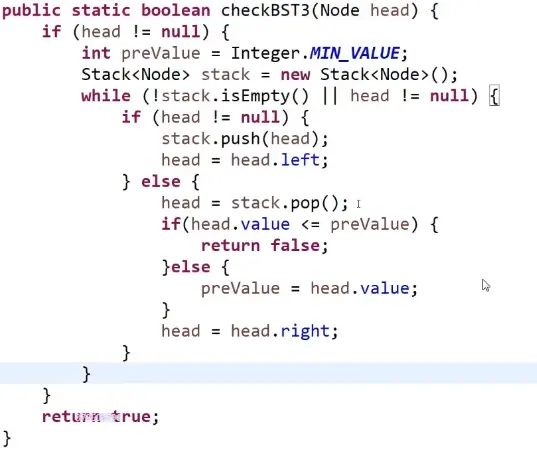
如何判断一棵树是完全二叉树
层遍历:
- 从左到右任意节点有右没左则false
- 在1的条件下,如果遇到了第一个左右子节点不全,则后续遇到的节点都必须皆为叶节点
public static boolean isCBT(Node head) {
if (head == null) {
return true;
}
LinkedList<Node> queue = new LinkedList<>();
boolean leaf = false;//是否遇到左右两个孩子不双全的节点
Node l = null;
Node r = null;
queue.add(head);
while (!queue.isEmpty()) {
head = queue.poll();
l = head.left;
r = head.right;
if ((leaf && (l != null || r != null)) || (l == null && r != null)) {
return false;
}
if (l != null) {
queue.add(l);
}
if (r != null) {
queue.add(r);
} else {
leaf = true;
}
}
return true;
}
如何判断是否是满二叉树
节点数=2^最大深度 -1

如何判断是否是平衡二叉树
public static boolean isBalanced(Node head) {
return process(head).isBalanced;
}
public static class ReturnType {
public boolean isBalanced;
public int height;
public ReturnType(boolean isB, int hei) {
isBalanced = isB;
height = hei;
}
}
public static ReturnType process(Node x) {
if (x == null) {
return new ReturnType(true, 0);
}
ReturnType leftData = process(x.left);
ReturnType rightData = process(x.right);
int height = Math.max(leftData.height, rightData.height);
boolean isBalanced = leftData.isBalanced && rightData.isBalanced
&& Math.abs(leftData.height - rightData.height) < 2;
return new ReturnType(isBalanced, height);
}
判断二叉树题目(树形DP)总结
平衡二叉树
- 左右子树必须为平衡二叉树
- (左树高度-右树高度) 的绝对值小于等于1
这时候我们就需要分析让左右子树提供哪些信息:
左子树:是否平衡,高度
右子树:是否平衡,高度
左右子树需求一样,所以递归解决
搜索二叉树
- 左BST ;左max < head
- 右BST;右min > head
需要的信息:
左树:是否BST,max
右树:是否BST,min
需求不一致,无法递归解决,需求改为统一:是否BST、max、min,再用递归统一解决

满二叉树
左:高度,节点数 ,右同左

给定两个二叉树的节点node1和node2,找到他们的最低公共祖先节点
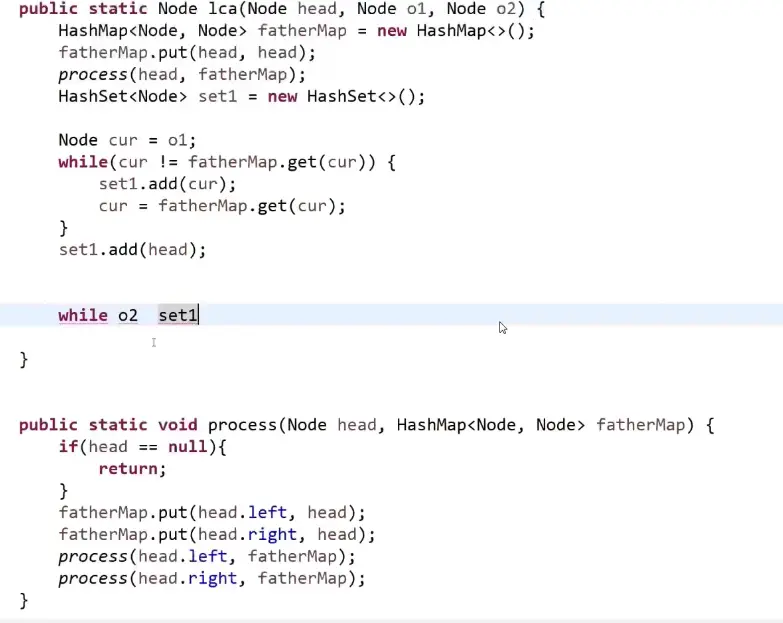
优化:
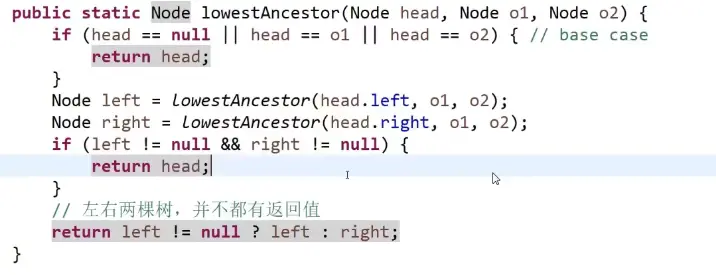
二叉树中找到一个节点的后续节点
【题目】 现在有一种新的二叉树节点类型如下: public class Node { public int value; public Node left; public Node right; public Node parent; public Node(int val) { value = val; } }
该结构比普通二叉树节点结构多了一个指向父节点的parent指针。 假设有一棵Node类型的节点组成的二叉树,树中每个节点的parent指针都正确地指向自己的父节点,头节 点的parent指向null。
只给一个在二叉树中的某个节点node,请实现返回node的后继节点的函数。 在二叉树的中序遍历的序列中, node的下一个节点叫作node的后继节点。
public static class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int data) {
this.value = data;
}
}
public static Node getSuccessorNode(Node node) {
if (node == null) {
return node;
}
if (node.right != null) {
return getLeftMost(node.right);//有右子树的时候,后继节点是其子树最左节点
} else {
Node parent = node.parent;
while (parent != null && parent.left != node) {//当前节点是其父亲的右孩子
node = parent;
parent = node.parent;
}
return parent;
}
}
public static Node getLeftMost(Node node) {
if (node == null) {
return node;
}
while (node.left != null) {
node = node.left;
}
return node;
}
二叉树的序列化和反序列化
就是内存里的一棵树如何变成字符串形式,又如何从字符串形式变成内存里的树
public static String serialByPre(Node head) {
if (head == null) {
return "#!";
}
String res = head.value + "!";
res += serialByPre(head.left);
res += serialByPre(head.right);
return res;
}
public static Node reconByPreString(String preStr) {
String[] values = preStr.split("!");
Queue<String> queue = new LinkedList<String>();
for (int i = 0; i != values.length; i++) {
queue.offer(values[i]);
}
return reconPreOrder(queue);
}
public static Node reconPreOrder(Queue<String> queue) {
String value = queue.poll();
if (value.equals("#")) {
return null;
}
Node head = new Node(Integer.valueOf(value));
head.left = reconPreOrder(queue);
head.right = reconPreOrder(queue);
return head;
}
public static String serialByLevel(Node head) {
if (head == null) {
return "#!";
}
String res = head.value + "!";
Queue<Node> queue = new LinkedList<Node>();
queue.offer(head);
while (!queue.isEmpty()) {
head = queue.poll();
if (head.left != null) {
res += head.left.value + "!";
queue.offer(head.left);
} else {
res += "#!";
}
if (head.right != null) {
res += head.right.value + "!";
queue.offer(head.right);
} else {
res += "#!";
}
}
return res;
}
public static Node reconByLevelString(String levelStr) {
String[] values = levelStr.split("!");
int index = 0;
Node head = generateNodeByString(values[index++]);
Queue<Node> queue = new LinkedList<Node>();
if (head != null) {
queue.offer(head);
}
Node node = null;
while (!queue.isEmpty()) {
node = queue.poll();
node.left = generateNodeByString(values[index++]);
node.right = generateNodeByString(values[index++]);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
return head;
}
public static Node generateNodeByString(String val) {
if (val.equals("#")) {
return null;
}
return new Node(Integer.valueOf(val));
}
如何判断一颗二叉树是不是另一棵二叉树的子树? 如何根据前序 中序遍历还原树之类问题
折纸问题
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后 展开。
此时折痕是凹下去的,即折痕突起的方向指向纸条的背面。 如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从 上到下依次是下折痕、下折痕和上折痕。 给定一个输入参数N,代表纸条都从下边向上方连续对折N次。 请从上到下打印所有折痕的方向。
例如:N=1时,打印: down N=2时,打印: down down up
public class Code10_PaperFolding {
public static void printAllFolds(int N) {
printProcess(1, N, true);
}
public static void printProcess(int i, int N, boolean down) {
if (i > N) {
return;
}
printProcess(i + 1, N, true);
System.out.println(down ? "down " : "up ");
printProcess(i + 1, N, false);
}
public static void main(String[] args) {
int N = 1;
printAllFolds(N);
}
}



